ALGUNS ESTADOS DE ENERGIAS DE GRACELI.
MOMENTUM. INERCIAL. ELETROMAGNÉTICO, TÉRMICO, DE CONDUTIVIDADE.
TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI
TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.
FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x [EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG
XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli + DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
número atômico, estrutura eletrônica, níveis de energia - TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- T l T l E l Fl dfG l
X [ESTADO QUÂNTICO]
XTODA FORMA DE EQUAÇÃO E FUNÇÃO EM:
Os campos de força estática são campos, como um simples campo elétrico , magnético ou gravitacional , que existem sem excitações. O método de aproximação mais comum que os físicos usam para cálculos de espalhamento pode ser interpretado como forças estáticas decorrentes das interações entre dois corpos mediadas por partículas virtuais , partículas que existem por apenas um curto período de tempo determinado pelo princípio da incerteza . [1] As partículas virtuais, também conhecidas como portadoras de força , são bósons , com diferentes bósons associados a cada força. [2]
A descrição de partículas virtuais de forças estáticas é capaz de identificar a forma espacial das forças, como o comportamento do inverso do quadrado na lei da gravitação universal de Newton e na lei de Coulomb . Também é capaz de prever se as forças são atrativas ou repulsivas para corpos semelhantes.
A formulação da integral do caminho é a linguagem natural para descrever os portadores de força. Este artigo usa a formulação integral de caminho para descrever os portadores de força para campos de spin 0, 1 e 2. Píons , fótons e grávitons se enquadram nessas respectivas categorias.
Existem limites para a validade da imagem da partícula virtual. A formulação de partícula virtual é derivada de um método conhecido como teoria de perturbação, que é uma aproximação assumindo que as interações não são muito fortes e foi planejado para problemas de espalhamento, não para estados ligados, como átomos. Para os quarks de ligação de força forte em núcleos em baixas energias, a teoria da perturbação nunca mostrou produzir resultados de acordo com os experimentos, [3] assim, a validade da imagem da "partícula mediadora de força" é questionável. Da mesma forma, para estados vinculados, o método falha. [4]Nestes casos, a interpretação física deve ser reexaminada. Por exemplo, os cálculos da estrutura atômica na física atômica ou da estrutura molecular na química quântica não poderiam ser facilmente repetidos, se tanto, usando a imagem da "partícula mediadora de força". [ citação necessária ]
O uso da imagem de "partícula mediadora de força" (FMPP) é desnecessário na mecânica quântica não relativística , e a lei de Coulomb é usada como dada na física atômica e química quântica para calcular os estados de ligação e de espalhamento. Uma teoria quântica relativística não perturbativa, em que a invariância de Lorentz é preservada, é alcançável avaliando a lei de Coulomb como uma interação de 4 espaços usando o vetor de posição de 3 espaços de um elétron de referência obedecendo à equação de Dirac e a trajetória quântica de um segundo elétron que depende apenas do tempo escalado. A trajetória quântica de cada elétron em um conjunto é inferida da corrente de Dirac para cada elétron, configurando-a igual a um campo de velocidade vezes uma densidade quântica, calculando um campo de posição a partir da integral de tempo do campo de velocidade e, finalmente, calculando uma trajetória quântica do valor esperado do campo de posição. As trajetórias quânticas são obviamente dependentes do spin e a teoria pode ser validada verificando se o Princípio de Exclusão de Pauli é obedecido para uma coleção de férmions.
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Os campos de força estática são campos, como um simples campo elétrico , magnético ou gravitacional , que existem sem excitações. O método de aproximação mais comum que os físicos usam para cálculos de espalhamento pode ser interpretado como forças estáticas decorrentes das interações entre dois corpos mediadas por partículas virtuais , partículas que existem por apenas um curto período de tempo determinado pelo princípio da incerteza . [1] As partículas virtuais, também conhecidas como portadoras de força , são bósons , com diferentes bósons associados a cada força. [2]
A descrição de partículas virtuais de forças estáticas é capaz de identificar a forma espacial das forças, como o comportamento do inverso do quadrado na lei da gravitação universal de Newton e na lei de Coulomb . Também é capaz de prever se as forças são atrativas ou repulsivas para corpos semelhantes.
A formulação da integral do caminho é a linguagem natural para descrever os portadores de força. Este artigo usa a formulação integral de caminho para descrever os portadores de força para campos de spin 0, 1 e 2. Píons , fótons e grávitons se enquadram nessas respectivas categorias.
Existem limites para a validade da imagem da partícula virtual. A formulação de partícula virtual é derivada de um método conhecido como teoria de perturbação, que é uma aproximação assumindo que as interações não são muito fortes e foi planejado para problemas de espalhamento, não para estados ligados, como átomos. Para os quarks de ligação de força forte em núcleos em baixas energias, a teoria da perturbação nunca mostrou produzir resultados de acordo com os experimentos, [3] assim, a validade da imagem da "partícula mediadora de força" é questionável. Da mesma forma, para estados vinculados, o método falha. [4]Nestes casos, a interpretação física deve ser reexaminada. Por exemplo, os cálculos da estrutura atômica na física atômica ou da estrutura molecular na química quântica não poderiam ser facilmente repetidos, se tanto, usando a imagem da "partícula mediadora de força". [ citação necessária ]
O uso da imagem de "partícula mediadora de força" (FMPP) é desnecessário na mecânica quântica não relativística , e a lei de Coulomb é usada como dada na física atômica e química quântica para calcular os estados de ligação e de espalhamento. Uma teoria quântica relativística não perturbativa, em que a invariância de Lorentz é preservada, é alcançável avaliando a lei de Coulomb como uma interação de 4 espaços usando o vetor de posição de 3 espaços de um elétron de referência obedecendo à equação de Dirac e a trajetória quântica de um segundo elétron que depende apenas do tempo escalado. A trajetória quântica de cada elétron em um conjunto é inferida da corrente de Dirac para cada elétron, configurando-a igual a um campo de velocidade vezes uma densidade quântica, calculando um campo de posição a partir da integral de tempo do campo de velocidade e, finalmente, calculando uma trajetória quântica do valor esperado do campo de posição. As trajetórias quânticas são obviamente dependentes do spin e a teoria pode ser validada verificando se o Princípio de Exclusão de Pauli é obedecido para uma coleção de férmions.
Forças clássicas [ editar ]
A força exercida por uma massa sobre outra e a força exercida por uma carga sobre outra são surpreendentemente semelhantes. Ambos caem conforme o quadrado da distância entre os corpos. Ambos são proporcionais ao produto das propriedades dos corpos, massa no caso da gravitação e carga no caso da eletrostática.
Eles também têm uma diferença notável. Duas massas se atraem, enquanto duas cargas semelhantes se repelem.
Em ambos os casos, os corpos parecem agir um sobre o outro à distância. O conceito de campo foi inventado para mediar a interação entre os corpos, eliminando assim a necessidade de ação a distância . A força gravitacional é mediada pelo campo gravitacional e a força de Coulomb é mediada pelo campo eletromagnético .
A força exercida por uma massa sobre outra e a força exercida por uma carga sobre outra são surpreendentemente semelhantes. Ambos caem conforme o quadrado da distância entre os corpos. Ambos são proporcionais ao produto das propriedades dos corpos, massa no caso da gravitação e carga no caso da eletrostática.
Eles também têm uma diferença notável. Duas massas se atraem, enquanto duas cargas semelhantes se repelem.
Em ambos os casos, os corpos parecem agir um sobre o outro à distância. O conceito de campo foi inventado para mediar a interação entre os corpos, eliminando assim a necessidade de ação a distância . A força gravitacional é mediada pelo campo gravitacional e a força de Coulomb é mediada pelo campo eletromagnético .
Força gravitacional [ editar ]
A força gravitacional em uma massa exercido por outra massa é
onde G é a constante gravitacional , r é a distância entre as massas, eé o vetor unitário da massa para a missa .
A força também pode ser escrita
Onde é o campo gravitacional descrito pela equação de campo
Onde é a densidade de massa em cada ponto do espaço.
A força gravitacional em uma massa exercido por outra massa é
onde G é a constante gravitacional , r é a distância entre as massas, eé o vetor unitário da massa para a missa .
A força também pode ser escrita
Onde é o campo gravitacional descrito pela equação de campo
Onde é a densidade de massa em cada ponto do espaço.
Força de Coulomb [ editar ]
A força eletrostática de Coulomb em uma carga exercido por uma carga é ( unidades SI )
Onde é a permissividade do vácuo , é a separação das duas cargas, e é um vetor unitário na direção da carga carregar .
A força Coulomb também pode ser escrita em termos de um campo eletrostático :
Onde
sendo a densidade de carga em cada ponto no espaço.
A força eletrostática de Coulomb em uma carga exercido por uma carga é ( unidades SI )
Onde é a permissividade do vácuo , é a separação das duas cargas, e é um vetor unitário na direção da carga carregar .
A força Coulomb também pode ser escrita em termos de um campo eletrostático :
Onde
sendo a densidade de carga em cada ponto no espaço.
Troca virtual de partículas [ editar ]
Na teoria da perturbação, as forças são geradas pela troca de partículas virtuais . A mecânica da troca de partículas virtuais é melhor descrita com a formulação integral de caminho da mecânica quântica. Existem insights que podem ser obtidos, no entanto, sem entrar no mecanismo das integrais de caminho, como por que as forças gravitacionais e eletrostáticas clássicas caem como o quadrado inverso da distância entre os corpos.
Na teoria da perturbação, as forças são geradas pela troca de partículas virtuais . A mecânica da troca de partículas virtuais é melhor descrita com a formulação integral de caminho da mecânica quântica. Existem insights que podem ser obtidos, no entanto, sem entrar no mecanismo das integrais de caminho, como por que as forças gravitacionais e eletrostáticas clássicas caem como o quadrado inverso da distância entre os corpos.
Formulação de caminho-integrante da troca virtual de partículas [ editar ]
Uma partícula virtual é criada por uma perturbação no estado de vácuo , e a partícula virtual é destruída quando é absorvida de volta ao estado de vácuo por outra perturbação. Imagina-se que os distúrbios se devem a corpos que interagem com o campo de partículas virtuais.
Uma partícula virtual é criada por uma perturbação no estado de vácuo , e a partícula virtual é destruída quando é absorvida de volta ao estado de vácuo por outra perturbação. Imagina-se que os distúrbios se devem a corpos que interagem com o campo de partículas virtuais.
A amplitude de probabilidade [ editar ]
Usando unidades naturais ,, a amplitude de probabilidade para a criação, propagação e destruição de uma partícula virtual é dada, na formulação integral de caminho por
Onde é o operador hamiltoniano , é o tempo decorrido, é a mudança de energia devido à perturbação, é a mudança na ação devido à perturbação, é o campo da partícula virtual, a integral está sobre todos os caminhos, e a ação clássica é dada por
Onde é a densidade Lagrangiana .
Aqui, a métrica do espaço - tempo é dada por
A integral do caminho muitas vezes pode ser convertida para a forma
Onde é um operador diferencial com e funções do espaço-tempo . O primeiro termo no argumento representa a partícula livre e o segundo termo representa a perturbação para o campo de uma fonte externa, como uma carga ou uma massa.
A integral pode ser escrita (consulte Integrais comuns na teoria quântica de campos )
Onde
é a mudança na ação devido aos distúrbios e ao propagador é a solução de
- .
Usando unidades naturais ,, a amplitude de probabilidade para a criação, propagação e destruição de uma partícula virtual é dada, na formulação integral de caminho por
Onde é o operador hamiltoniano , é o tempo decorrido, é a mudança de energia devido à perturbação, é a mudança na ação devido à perturbação, é o campo da partícula virtual, a integral está sobre todos os caminhos, e a ação clássica é dada por
Onde é a densidade Lagrangiana .
Aqui, a métrica do espaço - tempo é dada por
A integral do caminho muitas vezes pode ser convertida para a forma
Onde é um operador diferencial com e funções do espaço-tempo . O primeiro termo no argumento representa a partícula livre e o segundo termo representa a perturbação para o campo de uma fonte externa, como uma carga ou uma massa.
A integral pode ser escrita (consulte Integrais comuns na teoria quântica de campos )
Onde
é a mudança na ação devido aos distúrbios e ao propagador é a solução de
- .
Energia de interação [ editar ]
Assumimos que existem duas perturbações pontuais que representam dois corpos e que as perturbações são imóveis e constantes no tempo. Os distúrbios podem ser gravados
onde as funções delta estão no espaço, os distúrbios estão localizados em e , e os coeficientes e são os pontos fortes das perturbações.
Se negligenciarmos as auto-interações das perturbações, então W torna-se
- ,
que pode ser escrito
- .
Aqui é a transformada de Fourier de
- .
Finalmente, a mudança na energia devido às perturbações estáticas do vácuo é
.
Se essa quantidade for negativa, a força é atrativa. Se for positivo, a força é repulsiva.
Exemplos de correntes estáticas, imóveis e em interação são o Potencial Yukawa , o potencial Coulomb no vácuo e o potencial Coulomb em um plasma simples ou gás de elétron .
A expressão para a energia de interação pode ser generalizada para a situação em que as partículas pontuais estão se movendo, mas o movimento é lento em comparação com a velocidade da luz. Os exemplos são a interação de Darwin em um vácuo e a interação de Darwin em um plasma .
Finalmente, a expressão para a energia de interação pode ser generalizada para situações em que os distúrbios não são partículas pontuais, mas possivelmente cargas de linha, tubos de cargas ou vórtices de corrente. Os exemplos são Duas cargas de linha embutidas em um plasma ou gás de elétron , potencial Coulomb entre dois loops de corrente embutidos em um campo magnético e interação magnética entre os loops de corrente em um plasma simples ou gás de elétron . Como pode ser visto no exemplo de interação de Coulomb entre tubos de carga, mostrado abaixo, essas geometrias mais complicadas podem levar a fenômenos exóticos como números quânticos fracionários .
Assumimos que existem duas perturbações pontuais que representam dois corpos e que as perturbações são imóveis e constantes no tempo. Os distúrbios podem ser gravados
onde as funções delta estão no espaço, os distúrbios estão localizados em e , e os coeficientes e são os pontos fortes das perturbações.
Se negligenciarmos as auto-interações das perturbações, então W torna-se
- ,
que pode ser escrito
- .
Aqui é a transformada de Fourier de
- .
Finalmente, a mudança na energia devido às perturbações estáticas do vácuo é
.
Se essa quantidade for negativa, a força é atrativa. Se for positivo, a força é repulsiva.
Exemplos de correntes estáticas, imóveis e em interação são o Potencial Yukawa , o potencial Coulomb no vácuo e o potencial Coulomb em um plasma simples ou gás de elétron .
A expressão para a energia de interação pode ser generalizada para a situação em que as partículas pontuais estão se movendo, mas o movimento é lento em comparação com a velocidade da luz. Os exemplos são a interação de Darwin em um vácuo e a interação de Darwin em um plasma .
Finalmente, a expressão para a energia de interação pode ser generalizada para situações em que os distúrbios não são partículas pontuais, mas possivelmente cargas de linha, tubos de cargas ou vórtices de corrente. Os exemplos são Duas cargas de linha embutidas em um plasma ou gás de elétron , potencial Coulomb entre dois loops de corrente embutidos em um campo magnético e interação magnética entre os loops de corrente em um plasma simples ou gás de elétron . Como pode ser visto no exemplo de interação de Coulomb entre tubos de carga, mostrado abaixo, essas geometrias mais complicadas podem levar a fenômenos exóticos como números quânticos fracionários .
Exemplos selecionados [ editar ]
O potencial de Yukawa: A força entre dois núcleos em um núcleo atômico [ editar ]
Considere a densidade Lagrangiana de spin -0 [5]
- .
A equação de movimento para este Lagrangiano é a equação de Klein-Gordon
- .
Se adicionarmos uma perturbação, a amplitude de probabilidade torna-se
- .
Se integrarmos por partes e negligenciarmos os termos de fronteira no infinito, a amplitude de probabilidade torna-se
- .
Com a amplitude nesta forma pode-se perceber que o propagador é a solução de
- .
Disto pode-se ver que
- .
A energia devido aos distúrbios estáticos torna-se (consulte Integrais comuns na teoria quântica de campos )
com
que é atraente e tem uma variedade de
- .
Yukawa propôs que este campo descreve a força entre dois núcleos em um núcleo atômico. Isso lhe permitiu prever o alcance e a massa da partícula, agora conhecida como píon , associada a esse campo.
Considere a densidade Lagrangiana de spin -0 [5]
- .
A equação de movimento para este Lagrangiano é a equação de Klein-Gordon
- .
Se adicionarmos uma perturbação, a amplitude de probabilidade torna-se
- .
Se integrarmos por partes e negligenciarmos os termos de fronteira no infinito, a amplitude de probabilidade torna-se
- .
Com a amplitude nesta forma pode-se perceber que o propagador é a solução de
- .
Disto pode-se ver que
- .
A energia devido aos distúrbios estáticos torna-se (consulte Integrais comuns na teoria quântica de campos )
com
que é atraente e tem uma variedade de
- .
Yukawa propôs que este campo descreve a força entre dois núcleos em um núcleo atômico. Isso lhe permitiu prever o alcance e a massa da partícula, agora conhecida como píon , associada a esse campo.
Eletrostática [ editar ]
O potencial de Coulomb no vácuo [ editar ]
Considere o spin -1 Proca Lagrangiana com uma perturbação [6]
Onde
- ,
carga é conservada
- ,
e escolhemos o medidor Lorenz
- .
Além disso, assumimos que há apenas um componente semelhante ao tempo à perturbação. Na linguagem comum, isso significa que há uma carga nos pontos de perturbação, mas não há correntes elétricas.
Se seguirmos o mesmo procedimento que fizemos com o potencial Yukawa, descobriremos que
que implica
e
Isso produz
para o propagador do tempo e
que tem o sinal oposto ao caso Yukawa.
No limite da massa do fóton zero , o Lagrangiano se reduz ao Lagrangiano para eletromagnetismo
Portanto, a energia se reduz à energia potencial para a força de Coulomb e os coeficientes e são proporcionais à carga elétrica. Ao contrário do caso Yukawa, corpos semelhantes, neste caso eletrostático, se repelem.
Considere o spin -1 Proca Lagrangiana com uma perturbação [6]
Onde
- ,
carga é conservada
- ,
e escolhemos o medidor Lorenz
- .
Além disso, assumimos que há apenas um componente semelhante ao tempo à perturbação. Na linguagem comum, isso significa que há uma carga nos pontos de perturbação, mas não há correntes elétricas.
Se seguirmos o mesmo procedimento que fizemos com o potencial Yukawa, descobriremos que
que implica
e
Isso produz
para o propagador do tempo e
que tem o sinal oposto ao caso Yukawa.
No limite da massa do fóton zero , o Lagrangiano se reduz ao Lagrangiano para eletromagnetismo
Portanto, a energia se reduz à energia potencial para a força de Coulomb e os coeficientes e são proporcionais à carga elétrica. Ao contrário do caso Yukawa, corpos semelhantes, neste caso eletrostático, se repelem.
Coulomb potencial de uma forma simples de gás de plasma ou de electrões [ editar ]
Ondas de plasma [ editar ]
A relação de dispersão para ondas de plasma é [7]
Onde é a frequência angular da onda,
é a frequência do plasma ,é a magnitude da carga do elétron ,é a massa do elétron ,é a temperatura do elétron ( constante de Boltzmann igual a um), eé um fator que varia com frequência de um a três. Em altas frequências, na ordem da frequência do plasma, a compressão do fluido de elétrons é um processo adiabático eé igual a três. Em baixas frequências, a compressão é um processo isotérmico eé igual a um. Os efeitos de retardo foram negligenciados na obtenção da relação de dispersão das ondas de plasma.
Para baixas frequências, a relação de dispersão torna-se
Onde
é o número de Debye, que é o inverso do comprimento de Debye . Isso sugere que o propagador é
- .
Na verdade, se os efeitos de retardamento não forem negligenciados, então a relação de dispersão é
o que de fato produz o propagador adivinhado. Este propagador é igual ao propagador massivo de Coulomb com massa igual ao comprimento inverso de Debye. A energia de interação é, portanto,
O potencial Coulomb é rastreado em escalas de comprimento de um comprimento Debye.
A relação de dispersão para ondas de plasma é [7]
Onde é a frequência angular da onda,
é a frequência do plasma ,é a magnitude da carga do elétron ,é a massa do elétron ,é a temperatura do elétron ( constante de Boltzmann igual a um), eé um fator que varia com frequência de um a três. Em altas frequências, na ordem da frequência do plasma, a compressão do fluido de elétrons é um processo adiabático eé igual a três. Em baixas frequências, a compressão é um processo isotérmico eé igual a um. Os efeitos de retardo foram negligenciados na obtenção da relação de dispersão das ondas de plasma.
Para baixas frequências, a relação de dispersão torna-se
Onde
é o número de Debye, que é o inverso do comprimento de Debye . Isso sugere que o propagador é
- .
Na verdade, se os efeitos de retardamento não forem negligenciados, então a relação de dispersão é
o que de fato produz o propagador adivinhado. Este propagador é igual ao propagador massivo de Coulomb com massa igual ao comprimento inverso de Debye. A energia de interação é, portanto,
O potencial Coulomb é rastreado em escalas de comprimento de um comprimento Debye.
Plasmons [ editar ]
Em um gás de elétron quântico , as ondas de plasma são conhecidas como plasmons . A triagem Debye é substituída pela triagem Thomas-Fermi para produzir [8]
onde o inverso do comprimento de triagem Thomas-Fermi é
e é a energia Fermi
Esta expressão pode ser derivada do potencial químico para um gás de elétron e da equação de Poisson . O potencial químico para um gás de elétron próximo ao equilíbrio é constante e dado por
Onde é o potencial elétrico . Linearizar a energia de Fermi para a primeira ordem na flutuação da densidade e combiná-la com a equação de Poisson produz o comprimento de blindagem. O portador de força é a versão quântica da onda de plasma .
Em um gás de elétron quântico , as ondas de plasma são conhecidas como plasmons . A triagem Debye é substituída pela triagem Thomas-Fermi para produzir [8]
onde o inverso do comprimento de triagem Thomas-Fermi é
e é a energia Fermi
Esta expressão pode ser derivada do potencial químico para um gás de elétron e da equação de Poisson . O potencial químico para um gás de elétron próximo ao equilíbrio é constante e dado por
Onde é o potencial elétrico . Linearizar a energia de Fermi para a primeira ordem na flutuação da densidade e combiná-la com a equação de Poisson produz o comprimento de blindagem. O portador de força é a versão quântica da onda de plasma .
Duas cargas de linha incorporado em um gás de plasma ou de elétrons [ editar ]
Consideramos uma linha de carga com eixo na direção z embutida em um gás de elétron
Onde é a distância no plano xy da linha de carga, é a largura do material na direção z. O sobrescrito 2 indica que a função delta de Dirac está em duas dimensões. O propagador é
Onde é o comprimento de triagem Debye-Hückel inverso ou o comprimento de triagem Thomas-Fermi inverso .
A energia de interação é
Onde
e
são funções de Bessel eé a distância entre as duas cargas de linha. Para obter a energia de interação, usamos as integrais (consulte Integrais comuns na teoria quântica de campos )
e
Para , temos
Consideramos uma linha de carga com eixo na direção z embutida em um gás de elétron
Onde é a distância no plano xy da linha de carga, é a largura do material na direção z. O sobrescrito 2 indica que a função delta de Dirac está em duas dimensões. O propagador é
Onde é o comprimento de triagem Debye-Hückel inverso ou o comprimento de triagem Thomas-Fermi inverso .
A energia de interação é
Onde
e
são funções de Bessel eé a distância entre as duas cargas de linha. Para obter a energia de interação, usamos as integrais (consulte Integrais comuns na teoria quântica de campos )
e
Para , temos
Potencial de Coulomb entre dois circuitos de corrente incorporado em um campo magnético [ editar ]
Energia de interação de vórtices [ editar ]
Consideramos uma densidade de carga em tubo com eixo ao longo de um campo magnético embutido em um gás de elétron
Onde é a distância do centro guia , é a largura do material na direção do campo magnético
onde a frequência do cíclotron é ( unidades gaussianas )
e
é a velocidade da partícula em relação ao campo magnético e B é a magnitude do campo magnético. A fórmula da velocidade vem da definição da energia cinética clássica igual ao espaçamento entre os níveis de Landau no tratamento quântico de uma partícula carregada em um campo magnético.
Nesta geometria, a energia de interação pode ser escrita
Onde é a distância entre os centros dos loops atuais e
é uma função Bessel de primeiro tipo. Para obter a energia de interação, usamos a integral
Consideramos uma densidade de carga em tubo com eixo ao longo de um campo magnético embutido em um gás de elétron
Onde é a distância do centro guia , é a largura do material na direção do campo magnético
onde a frequência do cíclotron é ( unidades gaussianas )
e
é a velocidade da partícula em relação ao campo magnético e B é a magnitude do campo magnético. A fórmula da velocidade vem da definição da energia cinética clássica igual ao espaçamento entre os níveis de Landau no tratamento quântico de uma partícula carregada em um campo magnético.
Nesta geometria, a energia de interação pode ser escrita
Onde é a distância entre os centros dos loops atuais e
é uma função Bessel de primeiro tipo. Para obter a energia de interação, usamos a integral
Campo elétrico devido a uma perturbação densidade [ editar ]
O potencial químico próximo ao equilíbrio, é dado por
Onde é a energia potencial de um elétron em um potencial elétrico e e são o número de partículas no gás de elétron na ausência e na presença de um potencial eletrostático, respectivamente.
A flutuação da densidade é então
Onde é a área do material no plano perpendicular ao campo magnético.
A equação de Poisson produz
Onde
O propagador é então
e a energia de interação torna-se
onde na segunda igualdade ( unidades gaussianas ) assumimos que os vórtices tinham a mesma energia e a mesma carga do elétron.
Em analogia com os plasmons , o portador de força é a versão quântica da oscilação híbrida superior, que é uma onda de plasma longitudinal que se propaga perpendicularmente ao campo magnético.
O potencial químico próximo ao equilíbrio, é dado por
Onde é a energia potencial de um elétron em um potencial elétrico e e são o número de partículas no gás de elétron na ausência e na presença de um potencial eletrostático, respectivamente.
A flutuação da densidade é então
Onde é a área do material no plano perpendicular ao campo magnético.
A equação de Poisson produz
Onde
O propagador é então
e a energia de interação torna-se
onde na segunda igualdade ( unidades gaussianas ) assumimos que os vórtices tinham a mesma energia e a mesma carga do elétron.
Em analogia com os plasmons , o portador de força é a versão quântica da oscilação híbrida superior, que é uma onda de plasma longitudinal que se propaga perpendicularmente ao campo magnético.
Correntes com momento angular [ editar ]
Correntes de função Delta [ editar ]
Ao contrário das correntes clássicas, os loops de corrente quântica podem ter vários valores do raio de Larmor para uma determinada energia. [9] Os níveis de Landau , os estados de energia de uma partícula carregada na presença de um campo magnético, são multiplamente degenerados . Os loops de corrente correspondem aos estados de momento angular da partícula carregada que pode ter a mesma energia. Especificamente, a densidade de carga atinge o pico em torno de raios de
Onde é o número quântico do momento angular . Quandorecuperamos a situação clássica em que o elétron orbita o campo magnético no raio de Larmor . Se correntes de dois momentos angulares e interagir, e assumimos que as densidades de carga são funções delta no raio , então a energia de interação é
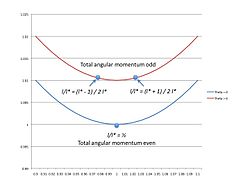
A energia de interação para é dado na Figura 1 para vários valores de . A energia para dois valores diferentes é fornecida na Figura 2.
Ao contrário das correntes clássicas, os loops de corrente quântica podem ter vários valores do raio de Larmor para uma determinada energia. [9] Os níveis de Landau , os estados de energia de uma partícula carregada na presença de um campo magnético, são multiplamente degenerados . Os loops de corrente correspondem aos estados de momento angular da partícula carregada que pode ter a mesma energia. Especificamente, a densidade de carga atinge o pico em torno de raios de
Onde é o número quântico do momento angular . Quandorecuperamos a situação clássica em que o elétron orbita o campo magnético no raio de Larmor . Se correntes de dois momentos angulares e interagir, e assumimos que as densidades de carga são funções delta no raio , então a energia de interação é
A energia de interação para é dado na Figura 1 para vários valores de . A energia para dois valores diferentes é fornecida na Figura 2.
Quasipartículas [ editar ]
Para grandes valores de momento angular, a energia pode ter mínimos locais em distâncias diferentes de zero e infinito. Pode-se verificar numericamente que os mínimos ocorrem em
Isso sugere que o par de partículas que são ligadas e separadas por uma distância atuar como uma única quasipartícula com momento angular.
Se escalarmos os comprimentos como , então a energia de interação se torna
Onde
O valor do em que a energia é mínima, , é independente da proporção . No entanto, o valor da energia no mínimo depende da relação. O menor mínimo de energia ocorre quando
Quando a razão difere de 1, o mínimo de energia é maior (Figura 3). Portanto, para valores pares de momento total, a menor energia ocorre quando (Figura 4)
ou
onde o momento angular total é escrito como
Quando o momento angular total é ímpar, os mínimos não podem ocorrer para Os estados de energia mais baixos para o momento angular total ímpar ocorrem quando
ou
e
que também aparecem como séries para o fator de preenchimento no efeito Hall quântico fracionário .
Para grandes valores de momento angular, a energia pode ter mínimos locais em distâncias diferentes de zero e infinito. Pode-se verificar numericamente que os mínimos ocorrem em
Isso sugere que o par de partículas que são ligadas e separadas por uma distância atuar como uma única quasipartícula com momento angular.
Se escalarmos os comprimentos como , então a energia de interação se torna
Onde
O valor do em que a energia é mínima, , é independente da proporção . No entanto, o valor da energia no mínimo depende da relação. O menor mínimo de energia ocorre quando
Quando a razão difere de 1, o mínimo de energia é maior (Figura 3). Portanto, para valores pares de momento total, a menor energia ocorre quando (Figura 4)
ou
onde o momento angular total é escrito como
Quando o momento angular total é ímpar, os mínimos não podem ocorrer para Os estados de energia mais baixos para o momento angular total ímpar ocorrem quando
ou
e
que também aparecem como séries para o fator de preenchimento no efeito Hall quântico fracionário .
A densidade de carga distribuídos por uma função de onda [ editar ]
A densidade de carga não está realmente concentrada em uma função delta. A carga é distribuída por uma função de onda. Nesse caso, a densidade do elétron é [10]
A energia de interação torna-se
Onde é uma função hipergeométrica confluente ou função de Kummer . Na obtenção da energia de interação, usamos a integral (consulte Integrais comuns na teoria quântica de campos )
Tal como acontece com os encargos da função delta, o valor de em que a energia é um mínimo local depende apenas do momento angular total, não dos momentos angulares das correntes individuais. Além disso, como acontece com as cargas da função delta, a energia no mínimo aumenta à medida que a proporção dos momentos angulares varia de um. Portanto, a série
e
aparecem também no caso de cargas espalhadas pela função de onda.
A função de onda de Laughlin é um ansatz para a função de onda quasipartícula. Se o valor esperado da energia de interação for assumido por uma função de onda de Laughlin , essas séries também serão preservadas.
A densidade de carga não está realmente concentrada em uma função delta. A carga é distribuída por uma função de onda. Nesse caso, a densidade do elétron é [10]
A energia de interação torna-se
Onde é uma função hipergeométrica confluente ou função de Kummer . Na obtenção da energia de interação, usamos a integral (consulte Integrais comuns na teoria quântica de campos )
Tal como acontece com os encargos da função delta, o valor de em que a energia é um mínimo local depende apenas do momento angular total, não dos momentos angulares das correntes individuais. Além disso, como acontece com as cargas da função delta, a energia no mínimo aumenta à medida que a proporção dos momentos angulares varia de um. Portanto, a série
e
aparecem também no caso de cargas espalhadas pela função de onda.
A função de onda de Laughlin é um ansatz para a função de onda quasipartícula. Se o valor esperado da energia de interação for assumido por uma função de onda de Laughlin , essas séries também serão preservadas.
Magnetostática [ editar ]
Darwin interacção no vácuo [ editar ]
Uma partícula carregada em movimento pode gerar um campo magnético que afeta o movimento de outra partícula carregada. A versão estática desse efeito é chamada de interação de Darwin . Para calcular isso, considere as correntes elétricas no espaço geradas por uma carga móvel
com uma expressão comparável para .
A transformada de Fourier desta corrente é
A corrente pode ser decomposta em uma parte transversal e uma longitudinal (ver decomposição de Helmholtz ).
O chapéu indica um vetor unitário . O último termo desaparece porque
que resulta da conservação de carga. Aqui desaparece porque estamos considerando forças estáticas.
Com a corrente nesta forma, a energia de interação pode ser escrita
- .
A equação do propagador para a Proca Lagrangiana é
A solução espacial é
que produz
que avalia (ver integrais comuns na teoria quântica de campos )
que se reduz a
no limite de pequeno m. A energia de interação é o negativo da interação Lagrangiana. Para duas partículas semelhantes viajando na mesma direção, a interação é atraente, o que é o oposto da interação de Coulomb.
Uma partícula carregada em movimento pode gerar um campo magnético que afeta o movimento de outra partícula carregada. A versão estática desse efeito é chamada de interação de Darwin . Para calcular isso, considere as correntes elétricas no espaço geradas por uma carga móvel
com uma expressão comparável para .
A transformada de Fourier desta corrente é
A corrente pode ser decomposta em uma parte transversal e uma longitudinal (ver decomposição de Helmholtz ).
O chapéu indica um vetor unitário . O último termo desaparece porque
que resulta da conservação de carga. Aqui desaparece porque estamos considerando forças estáticas.
Com a corrente nesta forma, a energia de interação pode ser escrita
- .
A equação do propagador para a Proca Lagrangiana é
A solução espacial é
que produz
que avalia (ver integrais comuns na teoria quântica de campos )
que se reduz a
no limite de pequeno m. A energia de interação é o negativo da interação Lagrangiana. Para duas partículas semelhantes viajando na mesma direção, a interação é atraente, o que é o oposto da interação de Coulomb.
Darwin interacção num plasma [ editar ]
Em um plasma, a relação de dispersão para uma onda eletromagnética é [11] ()
que implica
Aqui é a freqüência do plasma . A energia de interação é, portanto,
Em um plasma, a relação de dispersão para uma onda eletromagnética é [11] ()
que implica
Aqui é a freqüência do plasma . A energia de interação é, portanto,
Interacção magnética entre os circuitos de corrente de uma forma simples de gás de plasma ou de electrões [ editar ]
A energia de interação [ editar ]
Considere um tubo de corrente girando em um campo magnético embutido em um plasma simples ou gás de elétron. A corrente, que se encontra no plano perpendicular ao campo magnético, é definida como
Onde
e é o vetor unitário na direção do campo magnético. Aquiindica a dimensão do material na direção do campo magnético. A corrente transversal, perpendicular ao vetor de onda , impulsiona a onda transversal .
A energia da interação é
Onde é a distância entre os centros dos loops atuais e
é uma função Bessel de primeiro tipo. Para obter a energia de interação, usamos as integrais
e
Veja Integrais comuns na teoria quântica de campos .
Uma corrente em um plasma confinado ao plano perpendicular ao campo magnético gera uma onda extraordinária . [12] Esta onda gera correntes Hall que interagem e modificam o campo eletromagnético. A relação de dispersão para ondas extraordinárias é [13]
que dá para o propagador
Onde
em analogia com o propagador de Darwin. Aqui, a frequência híbrida superior é dada por
a frequência do ciclotron é dada por ( unidades gaussianas )
e a frequência do plasma ( unidades gaussianas )
Aqui n é a densidade do elétron, e é a magnitude da carga do elétron e m é a massa do elétron.
A energia de interação torna-se, para correntes,
Considere um tubo de corrente girando em um campo magnético embutido em um plasma simples ou gás de elétron. A corrente, que se encontra no plano perpendicular ao campo magnético, é definida como
Onde
e é o vetor unitário na direção do campo magnético. Aquiindica a dimensão do material na direção do campo magnético. A corrente transversal, perpendicular ao vetor de onda , impulsiona a onda transversal .
A energia da interação é
Onde é a distância entre os centros dos loops atuais e
é uma função Bessel de primeiro tipo. Para obter a energia de interação, usamos as integrais
e
Veja Integrais comuns na teoria quântica de campos .
Uma corrente em um plasma confinado ao plano perpendicular ao campo magnético gera uma onda extraordinária . [12] Esta onda gera correntes Hall que interagem e modificam o campo eletromagnético. A relação de dispersão para ondas extraordinárias é [13]
que dá para o propagador
Onde
em analogia com o propagador de Darwin. Aqui, a frequência híbrida superior é dada por
a frequência do ciclotron é dada por ( unidades gaussianas )
e a frequência do plasma ( unidades gaussianas )
Aqui n é a densidade do elétron, e é a magnitude da carga do elétron e m é a massa do elétron.
A energia de interação torna-se, para correntes,
Limite de pequena distância entre circuitos de corrente [ editar ]
No limite em que a distância entre os loops de corrente é pequena,
Onde
e
e I e K são funções de Bessel modificadas. presumimos que as duas correntes têm a mesma carga e velocidade.
Fizemos uso da integral (consulte Integrais comuns na teoria quântica de campos )
Para mr pequeno, o integral torna-se
Para mr grande, o integral torna-se
No limite em que a distância entre os loops de corrente é pequena,
Onde
e
e I e K são funções de Bessel modificadas. presumimos que as duas correntes têm a mesma carga e velocidade.
Fizemos uso da integral (consulte Integrais comuns na teoria quântica de campos )
Para mr pequeno, o integral torna-se
Para mr grande, o integral torna-se
Relação ao efeito Hall quântico [ editar ]
O número de onda de triagem pode ser escrito ( unidades gaussianas )
Onde é a constante de estrutura fina e o fator de preenchimento é
e N é o número de elétrons no material e A é a área do material perpendicular ao campo magnético. Este parâmetro é importante no efeito Hall quântico e no efeito Hall quântico fracionário . O fator de preenchimento é a fração de estados de Landau ocupados na energia do estado fundamental.
Para casos de interesse no efeito Hall quântico, é pequeno. Nesse caso, a energia de interação é
onde ( unidades gaussianas )
é a energia de interação para fator de preenchimento zero. Definimos a energia cinética clássica para a energia quântica
O número de onda de triagem pode ser escrito ( unidades gaussianas )
Onde é a constante de estrutura fina e o fator de preenchimento é
e N é o número de elétrons no material e A é a área do material perpendicular ao campo magnético. Este parâmetro é importante no efeito Hall quântico e no efeito Hall quântico fracionário . O fator de preenchimento é a fração de estados de Landau ocupados na energia do estado fundamental.
Para casos de interesse no efeito Hall quântico, é pequeno. Nesse caso, a energia de interação é
onde ( unidades gaussianas )
é a energia de interação para fator de preenchimento zero. Definimos a energia cinética clássica para a energia quântica
Gravitação [ editar ]
Um distúrbio gravitacional é gerado pelo tensor tensão-energia ; conseqüentemente, o Lagrangiano para o campo gravitacional é spin -2. Se os distúrbios estão em repouso, então o único componente do tensor tensão-energia que persiste é ocomponente. Se usarmos o mesmo truque de dar ao gráviton alguma massa e depois levar a massa a zero no final do cálculo, o propagador torna-se
e
,
que mais uma vez é atraente ao invés de repulsivo. Os coeficientes são proporcionais às massas das perturbações. No limite da pequena massa do gráviton, recuperamos o comportamento do inverso do quadrado da Lei de Newton. [14]
Ao contrário do caso eletrostático, no entanto, tomar o limite de pequena massa do bóson não produz o resultado correto. Um tratamento mais rigoroso produz um fator de um na energia em vez de 4/3. [15]
Um distúrbio gravitacional é gerado pelo tensor tensão-energia ; conseqüentemente, o Lagrangiano para o campo gravitacional é spin -2. Se os distúrbios estão em repouso, então o único componente do tensor tensão-energia que persiste é ocomponente. Se usarmos o mesmo truque de dar ao gráviton alguma massa e depois levar a massa a zero no final do cálculo, o propagador torna-se
e
,
que mais uma vez é atraente ao invés de repulsivo. Os coeficientes são proporcionais às massas das perturbações. No limite da pequena massa do gráviton, recuperamos o comportamento do inverso do quadrado da Lei de Newton. [14]
Ao contrário do caso eletrostático, no entanto, tomar o limite de pequena massa do bóson não produz o resultado correto. Um tratamento mais rigoroso produz um fator de um na energia em vez de 4/3. [15]
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC].
 + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
 + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL ![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCK

 [ESTADO QUÂNTICO]
[ESTADO QUÂNTICO]
















![Z \ equiv \ langle 0 | \ exp \ left (-i {\ hat H} T \ right) | 0 \ rangle = \ exp \ left (-iET \ right) = \ int D \ varphi \; \ exp \ left (i {\ mathcal {S}} [\ varphi] \ right) \; = \ exp \ left (iW \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/2151b70a2ba29798938e7f517e91c1373a5cd29e)





![{\ mathcal {S}} [\ varphi] = \ int {\ mathrm {d}} ^ {4} x \; {{\ mathcal {L}} [\ varphi (x)] \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63813174765f3c2470dbcd12f243413bf2a655a7)
![{\ mathcal {L}} [\ varphi (x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2365f42d88d429f1f0f926bfa9bd7deeb8c54db7)

![Z = \ int \ exp \ left [i \ int d ^ {4} x \ left ({\ frac 12} \ varphi {\ hat O} \ varphi + J \ varphi \ right) \ right] D \ varphi](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe8b3ee54150e5c533db5c3fbc0bf46a723bae3e)













![W \ left (J \ right) = - \ iint d ^ {4} x \; d ^ {4} y \; J_ {1} \ left (x \ right) {1 \ over 2} \ left [D \ esquerda (xy \ direita) + D \ esquerda (yx \ direita) \ direita] J_ {2} \ esquerda (y \ direita)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8920a2506fe0de48c5b849d2052b92bc29ab6f09)


![{1 \ over 2} \ left [D \ left (xy \ right) + D \ left (yx \ right) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/292c9f9aa03864ffaf187c8d724aa2b76ae35a34)

![{\ mathcal {L}} [\ varphi (x)] = {1 \ over 2} \ left [\ left (\ partial \ varphi \ right) ^ {2} -m ^ {2} \ varphi ^ {2} \direito]](https://wikimedia.org/api/rest_v1/media/math/render/svg/41d93ef0316977d86b8996f8f92fdcf9b4dbfe7d)

![Z = \ int D \ varphi \; \ exp \ left \ {i \ int d ^ {4} x \; \ left [{1 \ over 2} \ left (\ left (\ partial \ varphi \ right) ^ { 2} -m ^ {2} \ varphi ^ {2} \ right) + J \ varphi \ right] \ right \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2546ebbc13d0451682853cc36fd9b1b2a01267a)
![Z = \ int D \ varphi \; \ exp \ left \ {i \ int d ^ {4} x \; \ left [- {1 \ over 2} \ varphi \ left (\ partial ^ {2} + m ^ {2} \ right) \ varphi + J \ varphi \ right] \ right \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dea41e0c54b700ba60bb1e7024df724f298571ba)





![{\ mathcal {L}} [\ varphi (x)] = - {1 \ over 4} F _ {{\ mu \ nu}} F ^ {{\ mu \ nu}} + {1 \ over 2} m ^ {2} A _ {{\ mu}} A ^ {{\ mu}} + A _ {{\ mu}} J ^ {{\ mu}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591ac6f78391e4d0d1a0b85785580bb271acd6a0)


































































































![{\ vec J} _ {1} \ left ({\ vec k} \ right) = a_ {1} \ left [1 - {\ hat k} {\ hat k} \ right] \ cdot {\ vec v} _ {1} \ exp \ left (i {\ vec k} \ cdot {\ vec x} _ {1} \ right) + a_ {1} \ left [{\ hat k} {\ hat k} \ right] \ cdot {\ vec v} _ {1} \ exp \ left (i {\ vec k} \ cdot {\ vec x} _ {1} \ right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0d79a6445282ae388d82ee449b22ed22e6d1b1b)


![E = a_ {1} a_ {2} \ int {d ^ {3} k \ over (2 \ pi) ^ {3}} \; \; D \ left (k \ right) \ mid _ {{k_ { 0} = 0}} \; {\ vec v} _ {1} \ cdot \ left [1 - {\ hat k} {\ hat k} \ right] \ cdot {\ vec v} _ {2} \; \ exp \ left (i {\ vec k} \ cdot \ left (x_ {1} -x_ {2} \ right) \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/b31cb210dde9aae552bd4602f092777182990c7b)


![E = -a_ {1} a_ {2} \ int {d ^ {3} k \ over (2 \ pi) ^ {3}} \; \; {{\ vec v} _ {1} \ cdot \ left [1 - {\ hat k} {\ hat k} \ right] \ cdot {\ vec v} _ {2} \ over {\ vec k} ^ {2} + m ^ {2}} \; \ exp \ esquerda (i {\ vec k} \ cdot \ esquerda (x_ {1} -x_ {2} \ direita) \ direita)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9871a14a8457fef3cb44a14f461235eaef662678)
![E = - {1 \ over 2} {a_ {1} a_ {2} \ over 4 \ pi r} e ^ {{- mr}} \ left \ {{2 \ over \ left (mr \ right) ^ { 2}} \ left (e ^ {{mr}} - 1 \ right) - {2 \ over mr} \ right \} {\ vec v} _ {1} \ cdot \ left [1 + {{\ hat r }} {{\ hat r}} \ right] \ cdot {\ vec v} _ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28c0e2cb7cceec027934b6da5ac7116cd6fe0ce9)
![E = - {1 \ over 2} {a_ {1} a_ {2} \ over 4 \ pi r} {\ vec v} _ {1} \ cdot \ left [1 + {{\ hat r}} {{ \ hat r}} \ right] \ cdot {\ vec v} _ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe161e44ff7d95dcc83d5a55939ae0f7a09e932)




![E = - {1 \ over 2} {a_ {1} a_ {2} \ over 4 \ pi r} {\ vec v} _ {1} \ cdot \ left [1 + {{\ hat r}} {{ \ hat r}} \ right] \ cdot {\ vec v} _ {2} \; e ^ {{- \ omega _ {p} r}} \ left \ {{2 \ over \ left (\ omega _ { p} r \ right) ^ {2}} \ left (e ^ {{\ omega _ {p} r}} - 1 \ right) - {2 \ over \ omega _ {p} r} \ right \}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/11a047fded9d15e84ef56661d2ba389d2eaac59e)
















![I_ {1} \ left (mr \ right) K_ {1} \ left (mr \ right) \ rightarrow {1 \ over 2} \ left [1- {1 \ over 8} \ left (mr \ right) ^ { 2} \ right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/e390202b2aefd0672891fb96523c9102e6177d08)





![E = - {E_ {0} \ over 2} \ left [1- {1 \ over 8} \ mu ^ {2} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c296979564d5355f378e0b6dabd44ef0aeeba314)






Comentários
Postar um comentário